Using Norton theorem, find the equivalent Norton circuit for the highlighted circuit aross terminals a-b.
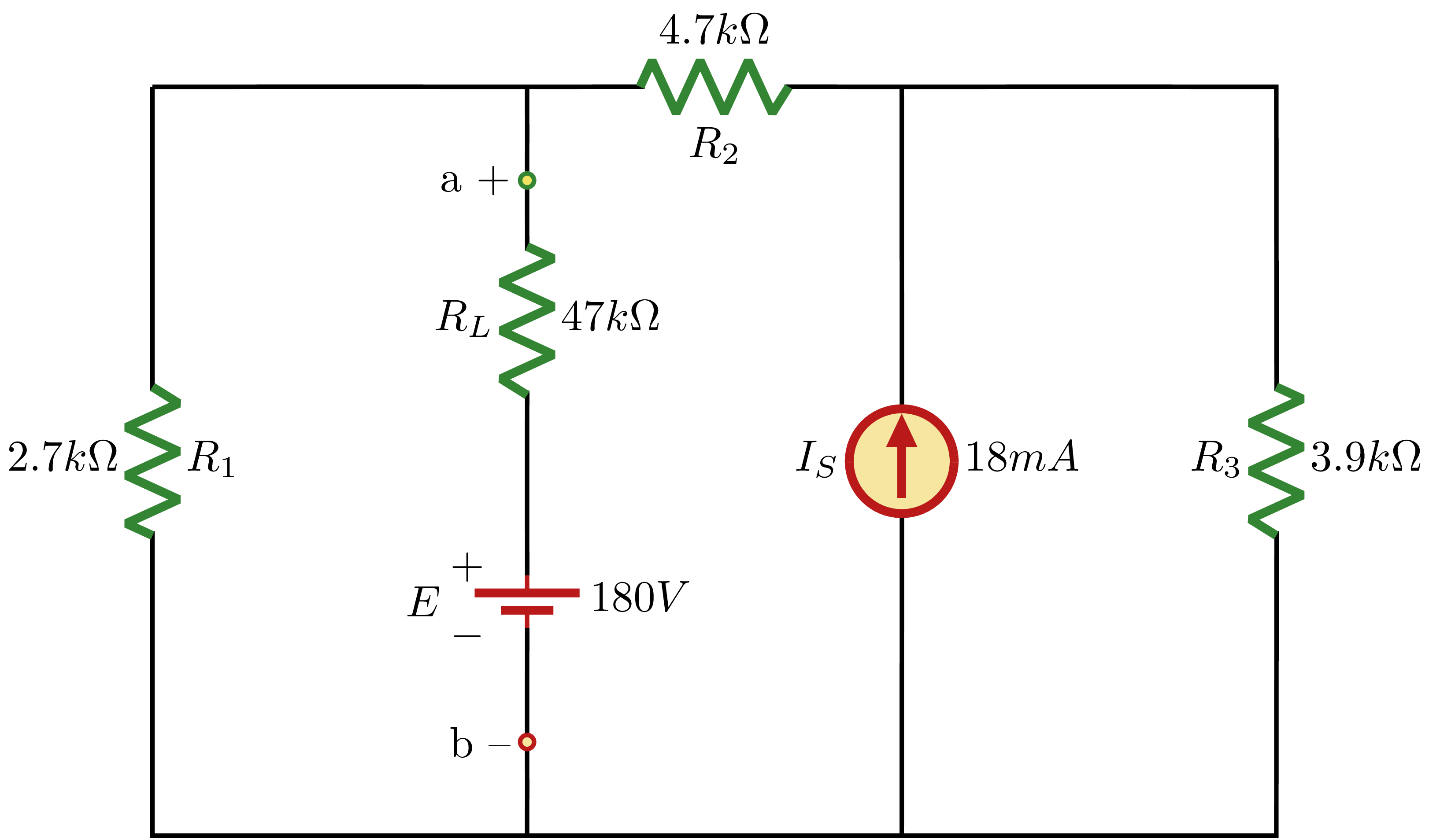
Solving for $R_{N}$
$$\begin{align}
R_{N} &= R_1 //(R_2 + R_3)\\
&= \frac{(2.7k\Omega) \cdot (4.7k\Omega+3.9k\Omega)}{(2.7k\Omega) + (4.7k\Omega + 3.9k\Omega)} \\
&= \frac{(2.7) \cdot (8.6)}{11.3}k\Omega \\
&=2.055k\Omega
\end{align}
$$
Solving for $I_N$
$$\begin{align}
\text{Using current divider rule:} \rightarrow I_{N} &= \frac{R_3}{R_2 + R_3}\cdot I_s\\
&= \frac{3.9k\Omega}{4.7k\Omega + 3.9k\Omega}\cdot 18mA\\
&= 0.4535\cdot 18mA\\
&=8.163mA
\end{align}
$$