Dr. AlSharidah

CTSEET is the documentation website for courses offered by Dr. M. E. AlSharidah. It records all course descriptions, learning outcomes, objectives, syllabus, and notes.

70-115: Electric Circuits

Description:

This course starts with presentation of source conversion. The chapters thereafter focus on the fundamental theorems of DC electrical network such as mesh analysis, nodal analysis, superposition, Thevenin's and Norton's theorems, maximum power transfer and finally Millman's theorem. The same theorems are repeated for AC electrical networks. Finally, methods for analyzing and calculating electrical quantities of balanced three-phase systems will be discussed.

Textbook:

Robert L. Boylestad, "Introductory Circuit Analysis".

70-115: Elecrtric Circuits ¹

Important dates:

Attendance and Absence:

1. Commitment to attendance is required, and absences must not exceed 12 hours to avoid being barred from the course.
2. Every 4 hours of absence will result in a 25% deduction from the attendance grade.
3. Any medical excuse (official from the relevant authorities) must be submitted before the absence from the lecture, except in emergency cases.
4. No medical excuse will be accepted unless it prevents you from attending class or accessing the Teams platform.
5. Attendance will be recorded within the first 10 minutes of the lecture or the beginning of the meeting created for the lecture.

Assignment and Report Submission:

1. Assignments and reports must be submitted according to the specified conditions and deadlines.
2. Any delay in submitting assignments or reports will result in a 5% deduction from the grade for every hour of delay.
3. All submitted assignments and reports must be the student's personal work and performance only.
4. Plagiarism, copying, or cheating in assignments or reports, including purchasing assignments or reports, will result in failing the course.

Student Ethical Responsibility:

1. The student is fully responsible for the course requirements and must work hard and diligently to pass the course with distinction.
2. Passing or failing the course may determine the student's graduation date.
3. Everything mentioned above is part of the student's responsibility, and they must bear the full consequences.

Course Objectives

1. Analyze DC electric circuits using superposition theorem.

   1. Understand the difference between voltage and current sources when apply the theorem.
   2. Current and voltage sources transformation.
   3. Apply the superposition theorem in DC circuits.
   4. Use basic laboratory measurement equipment including the power supplies, digital multimeters, function generators, and oscilloscopes to conduct experiments.

   ---

2. Analyze DC electric circuits using thevenin's theorem.

   1. Calculate Thevinens equivalent resistance.
   2. Calculate Thevinens equivalent voltage source.
   3. Apply Thevinens theorem to find the current and voltage at load.
   4. State the vale of load resistance for maximum power condition.
   5. Use basic laboratory measurement equipment including the power supplies, digital multimeters, function generators, and oscilloscopes to conduct experiments.

   ---

3. Analyze DC electric circuits using mesh analysis.

   1. Write the mesh equations.
   2. Solve the mesh equations using matrix calculations.
   3. Use basic laboratory measurement equipment including the power supplies, digital multimeters, function generators, and oscilloscopes to conduct experiments.

   ---

4. Analyze DC electric circuits using node analysis.

   1. Write the node equations.
   2. Solve the node equations using matrix calculations.
   3. Use basic laboratory measurement equipment including the power supplies, digital multimeters, function generators, and oscilloscopes to conduct experiments.

   ---

5. Analyze AC electric circuits using superposition theorem.

   1. Understand the concepts of Fourier series and its application in circuit analysis.
   2. Compute the Fourier series for continuous-time periodic signals and apply frequency domain method of circuit analysis.
   3. Calculate rms value and harmonic content of a periodic waveform.
   4. Use computer simulation (Matlab and/or Pspice) tools to design and analyze simple circuits

   ---

6. Analyze AC electric circuits using Thevenin's theorem.

   1. Calculate Thevinens equivalent impedance
   2. Identify the value of load impedance for maximum power condition.
   3. Calculate Thevinens equivalent voltage source.
   4. Apply Thevinens theorem to find the current and voltage at load.
   5. Use basic laboratory measurement equipment including the power supplies, digital multimeters, function generators, and oscilloscopes to conduct experiments.

   ---

7. Analyze AC electric circuits using mesh analysis.

   1. Write the mesh equations.
   2. Solve the mesh equations using matrix calculations.
   3. Use basic laboratory measurement equipment including the power supplies, digital multimeters, function generators, and oscilloscopes to conduct experiments.

   ---

8. Analyze AC electric circuits using node analysis.

   1. Write the mesh equations.
   2. Solve the mesh equations using matrix calculations.
   3. Use basic laboratory measurement equipment including the power supplies, digital multimeters, function generators, and oscilloscopes to conduct experiments.

   ---

9. Recognize the basic voltages and currents relations in balanced three phase electric circuits.
   1. Recognize three phase electric circuits, Delta and Star connections
   2. Differentiate between the line and phase values
   3. Calculate the current in three phase balanced load, delta connection
   4. Calculate the current in three phase balanced load, star connection

The following selected chapters give in depth explanation on subjects related to the course.

All course lecture and labs recorded meetings and notes

Lecture Notes

Mesh analysis example

Lectures and Labs on Microsoft Stream

Using superposition, find the current through $R_1$

Simulation:

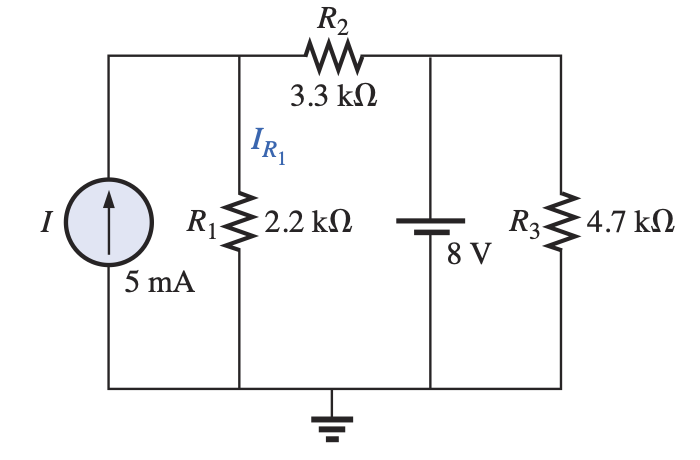
Using simulation as a guide, the circuit parameters will be as in the figue below.

Solution:

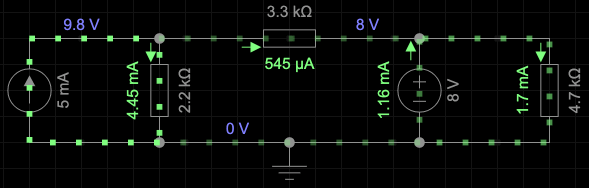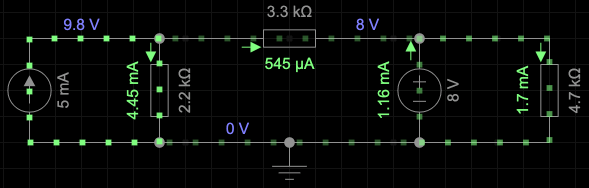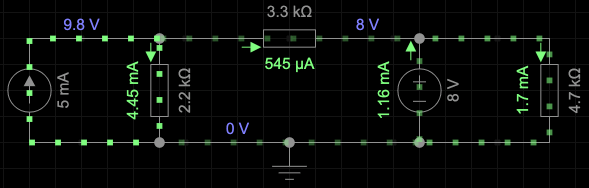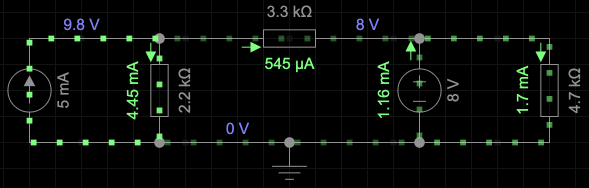
The solution is in two parts. First we turn the battery off and solve for the current in $R_1$. The second part, we turn off the current source and solve for the curent through $R_1$ due to the battery.

Step 1: I (ON) E (OFF)

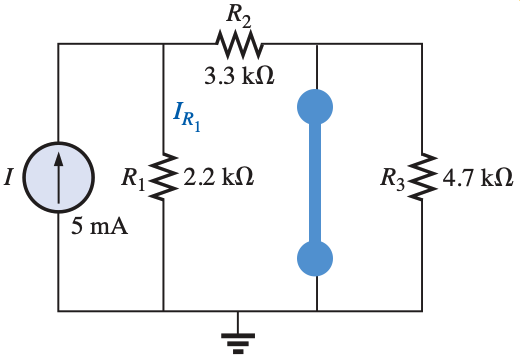
Note that $R_3$ is shorted, and to obtain the current through $R_1$ we will use the current divider rule:

$$\begin{align}\text{Current divider rule: }\rightarrow I'_{R_1} &= \frac{R_2}{(R_1+R_2)}\cdot I \\
&=\frac{3.3 k\Omega}{(2.2 k\Omega + 3.3k\Omega)}\cdot 5mA \\
&=\frac{3.3 k\Omega}{5.5 k\Omega }\cdot 5mA \\
&=0.6\cdot 5mA \\
&=3mA \end{align}$$

Step 2: I (OFF) E (ON)

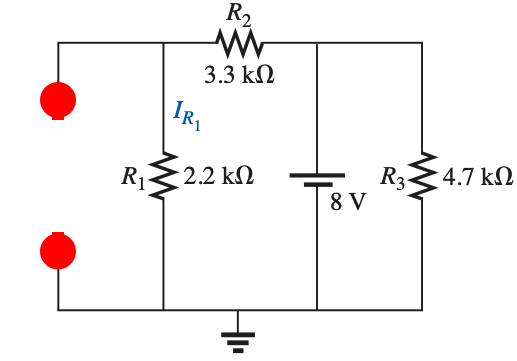
Since $R_3$ is in parallel with the battery, then the voltage across it is the battery voltage and it wont affect the current through $R_1$.
To solver for the current through $R_1$, we will only consider the resistances on the left side of the battery

$$\begin{align}\text{Ohm's Law: }\rightarrow I''_{R_1} &= \frac{E}{(R_1+R_2)}\\
&=\frac{8V}{(2.2 k\Omega + 3.3k\Omega)}\\
&=\frac{8V}{5.5 k\Omega }\\
&=1.455 mA \\
&=1.46 mA \end{align}$$

Step 3: Solving for $I_{R_1}$

$$\begin{align*}I_{R_1} &= I'_{R_1} + I''_{R_1} \\
&= 3 mA + 1.46 mA\\
&= 4.46 mA\end{align*}$$

Using superposition, find the voltage $V_2$ across the $6.8k\Omega$ resistor for the network of the figue below.

which is the same as

Simulation:

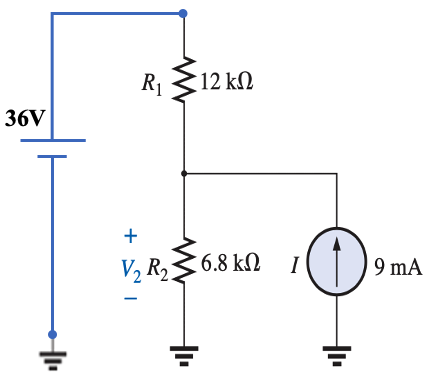
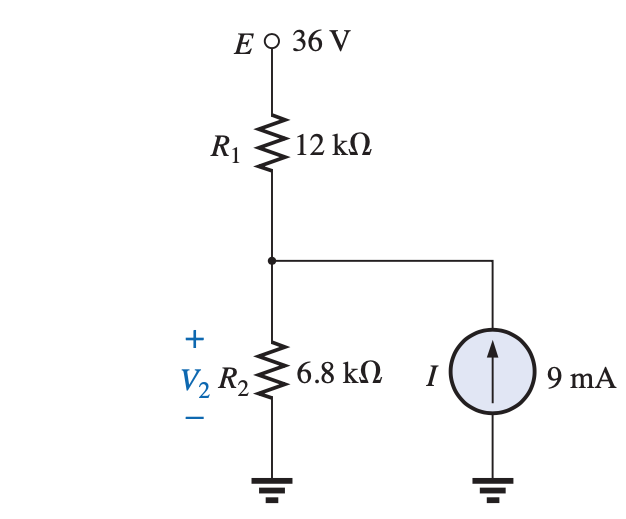
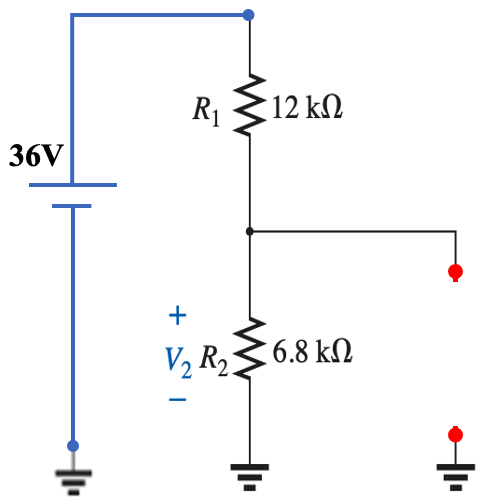
Using simulation as a guide, the circuit parameters will be as in the figue below.

Solution:

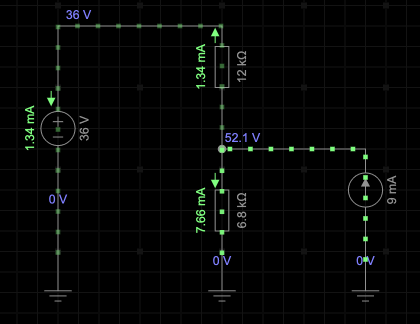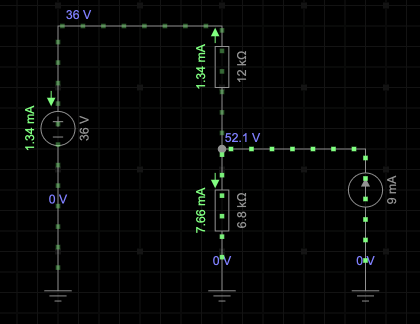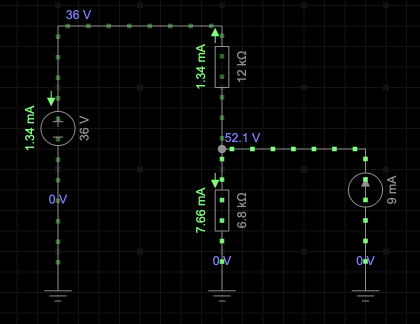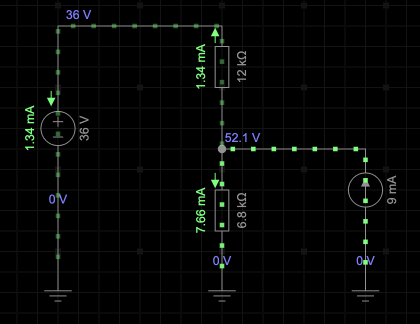
First we turn the battery off and solve for the voltage $V'_2$ across $R_2$. Then we turn off the current source $I$ and solve for the $V''_2$ due to the 36V battery.

Step 1: I (ON) E (OFF)

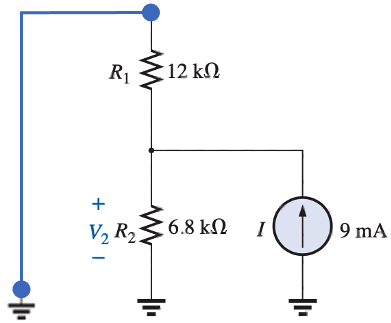
We can use the current divider rule to find the current through $R_2$ then use Ohm's law to find the voltage $V_2$:

$$\begin{align}\text{Current divider rule: }\rightarrow I'_{2} &= \frac{R_1}{(R_1+R_2)}\cdot I \\
&=\frac{12 k\Omega}{(12 k\Omega + 6.8k\Omega)}\cdot 9mA \\
&=\frac{12 k\Omega}{18.8 k\Omega }\cdot 9mA \\
&=0.638\cdot 9mA \\
&=5.745mA\\
\text{Ohm's law: }\rightarrow V'_2 &= R_2 \cdot I'_{2}\\
&=6.8k\Omega \cdot 5.75mA\\
&=(6.8\times 10^3) \cdot (5.75\times 10^{-3})\\
&= 39.06 V\end{align}$$

Step 2: I (OFF) E (ON)

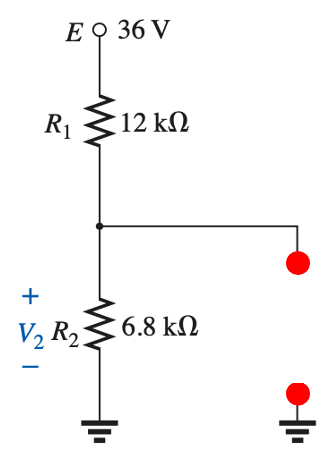
which is equivalent to

Since $R_3$ is in parallel with the battery, then the voltage across it is the battery voltage and it wont affect the current through $R_1$.
To solver for the current through $R_1$, we will only consider the resistances on the left side of the battery

$$\begin{align}\text{Voltage divider rule: }\rightarrow V''_{2} &= \frac{R_2}{(R_1+R_2)}\cdot E\\
&=\frac{6.8 k\Omega}{(12 k\Omega + 6.8 k\Omega)} \cdot 36 V\\
&=\frac{6.8 k\Omega}{18.8 k\Omega } \cdot 36 V\\
&= 13.02 V \end{align}$$

Step 3: Solving for $V_2$

$$\begin{align*} V_2 &= V'_2 + V''_2 \\
&= 39.06 V + 13.02 V\\
&= 52.08 V \end{align*}$$

Using Thevenin theorem, find the equivalent Thevenin circuit for the highlighted circuit from the a-b terminals.

Solving for $R_{TH}$

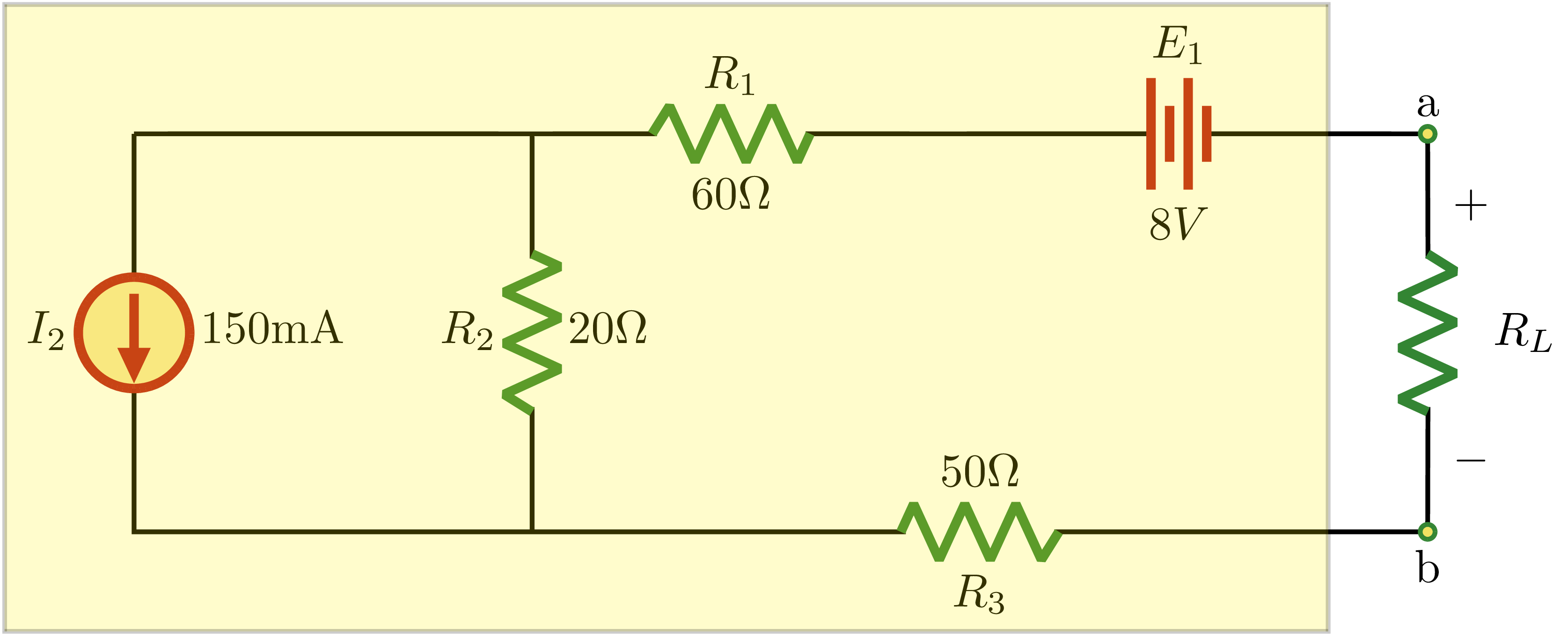
$$\begin{align}
R_{TH} &= R_1 + R_2 + R_3\\
&= 60\Omega + 20\Omega + 50\Omega \\
&= 130\Omega
\end{align}
$$

Solving for $E_{TH}$

$$\begin{align}
E_{TH} &= -E_1 -R_2\cdot I_2\\
&= -8V - (20\Omega) \cdot (150 mA)\\
&= -8V - 3V\\
&= -11V
\end{align}
$$

Using Thevenin theorem, find the equivalent Thevenin circuit for the highlighted circuit external to $R_L$.

Solving for $R_{TH}$

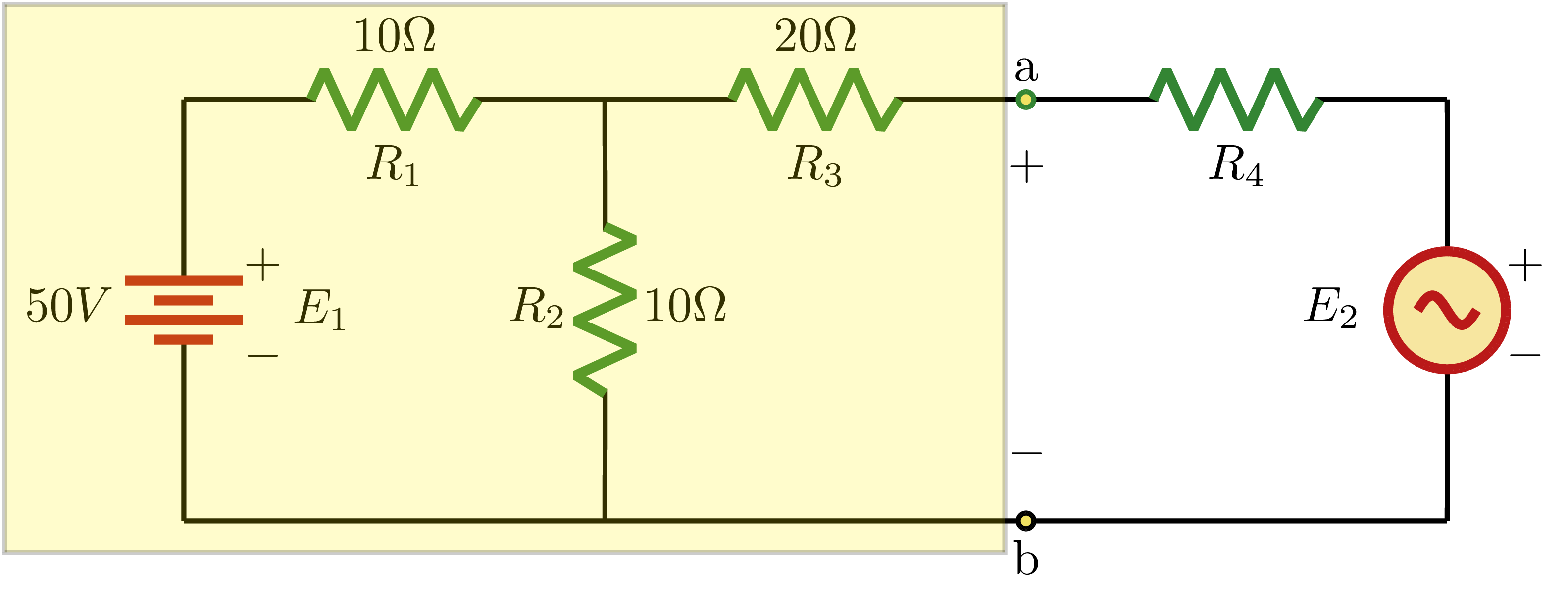
$$\begin{align}
R_{TH} &= (R_1 //R_2) + R_3\\
&= \frac{10\Omega}{2} + 20\Omega \\
&= 25\Omega
\end{align}
$$

Solving for $E_{TH}$

$$\begin{align}
\text{Voltage divider rule:} \rightarrow E_{TH} &= \frac{R_2}{R_1+R_2} \cdot E_1\\
&= \frac{10\Omega}{(10+10)\Omega}\cdot 50V\\
&= \frac{10\Omega}{20\Omega}\cdot 50V\\
&= 25V
\end{align}
$$

Using Norton theorem, find the equivalent Norton circuit for the highlighted circuit aross terminals a-b.

Solving for $R_{N}$

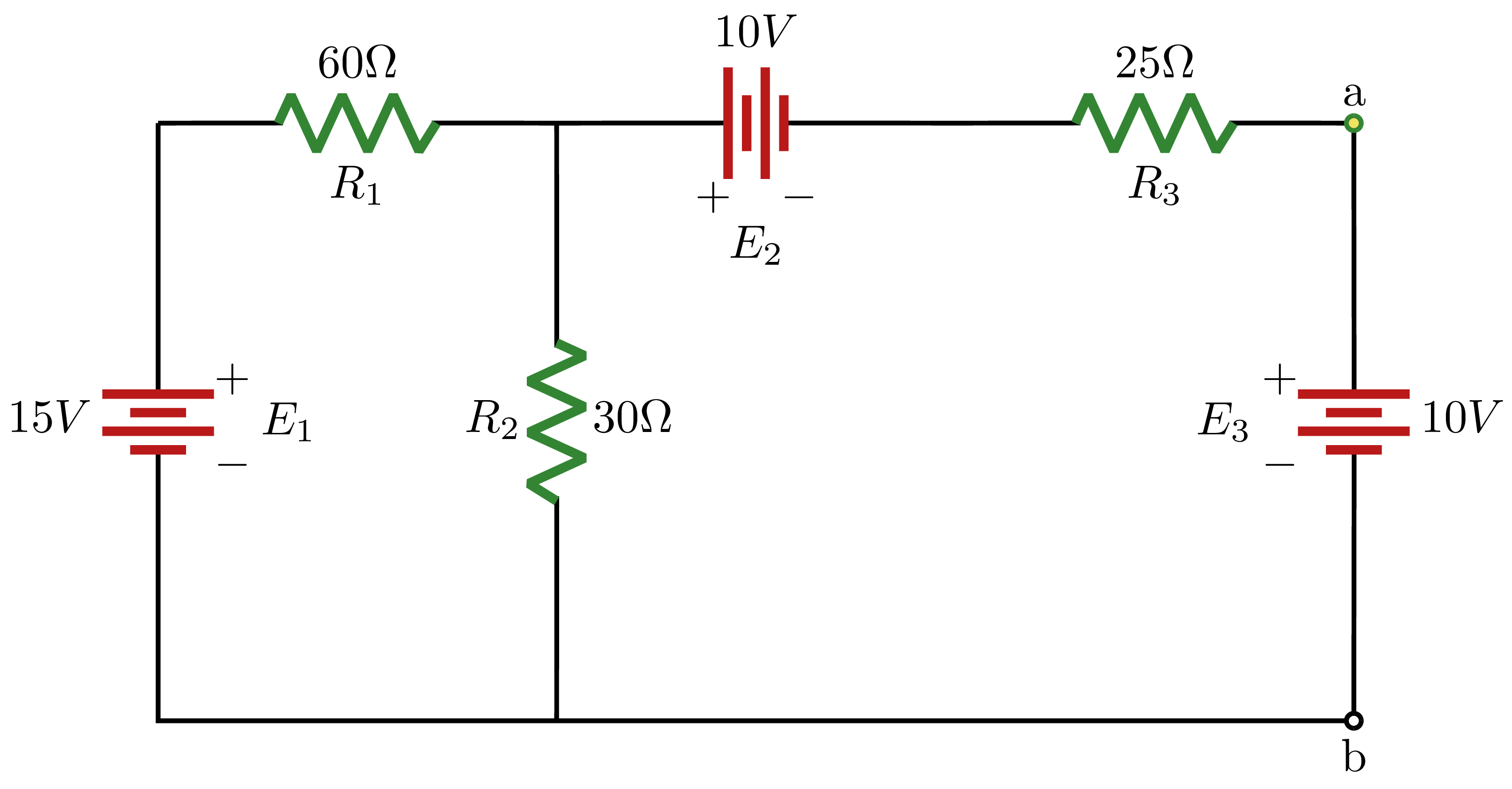
$$\begin{align}
R_{N} &= (R_1 //R_2) + R_3\\
&= \frac{(60\Omega) \cdot (30 \Omega)}{(60\Omega) + (30 \Omega)} + 25\Omega \\
&= 20\Omega + 25\Omega \\
&=45\Omega
\end{align}
$$

Using superposition to solve for $I_N$

$I'_N$: $E_1$ ON $E_2$ OFF

$$\begin{align}
\text{Solve for the voltage across $R_2$//$R_3$:} \rightarrow R_{23} &= \frac{R_2 \cdot R_3}{R_2 + R_3}\\
&= \frac{(30\Omega) \cdot (25\Omega)}{30\Omega + 25\Omega}\\
&= 13.64\Omega\\
\rightarrow V_{23} &= \frac{R_{23}}{R_1+R_{23}}\cdot E_1\\
&=\frac{13.64\Omega}{(60+13.64)\Omega}\cdot 15V\\
&=\frac{13.64}{73.64}\Omega\cdot 15V\\
&=2.778V\\
\therefore I'_N &= \frac{V_{23}}{R_3}\\
&=\frac{2.778V}{25\Omega}\\
&=111.1 mA
\end{align}
$$

$I''_N$: $E_1$ OFF $E_2$ ON

$$\begin{align}
\text{Solve for the total resistance:} \rightarrow R_{T} &= R_1 // R_2 + R_3\\
&=\frac{R_1 \cdot R_2}{R_1 + R_2}+R_3\\
&= \frac{(60\Omega) \cdot (30\Omega)}{60\Omega + 30\Omega}+25\Omega\\
&= 20\Omega+ 25\Omega\\
&=45\Omega\\
\therefore I''_N &= \frac{-E_{2}}{R_T}\\
&=\frac{-10V}{45\Omega}\\
&=-222.2 mA
\end{align}
$$

Solving for $I_N$

$$\begin{align}
I_N &= I'_N - I''_N\\
&=111.1mA - 222.2mA\\
&=-111.1 mA
\end{align}
$$

Using Norton theorem, find the equivalent Norton circuit for the highlighted circuit aross terminals a-b.

Solving for $R_{N}$

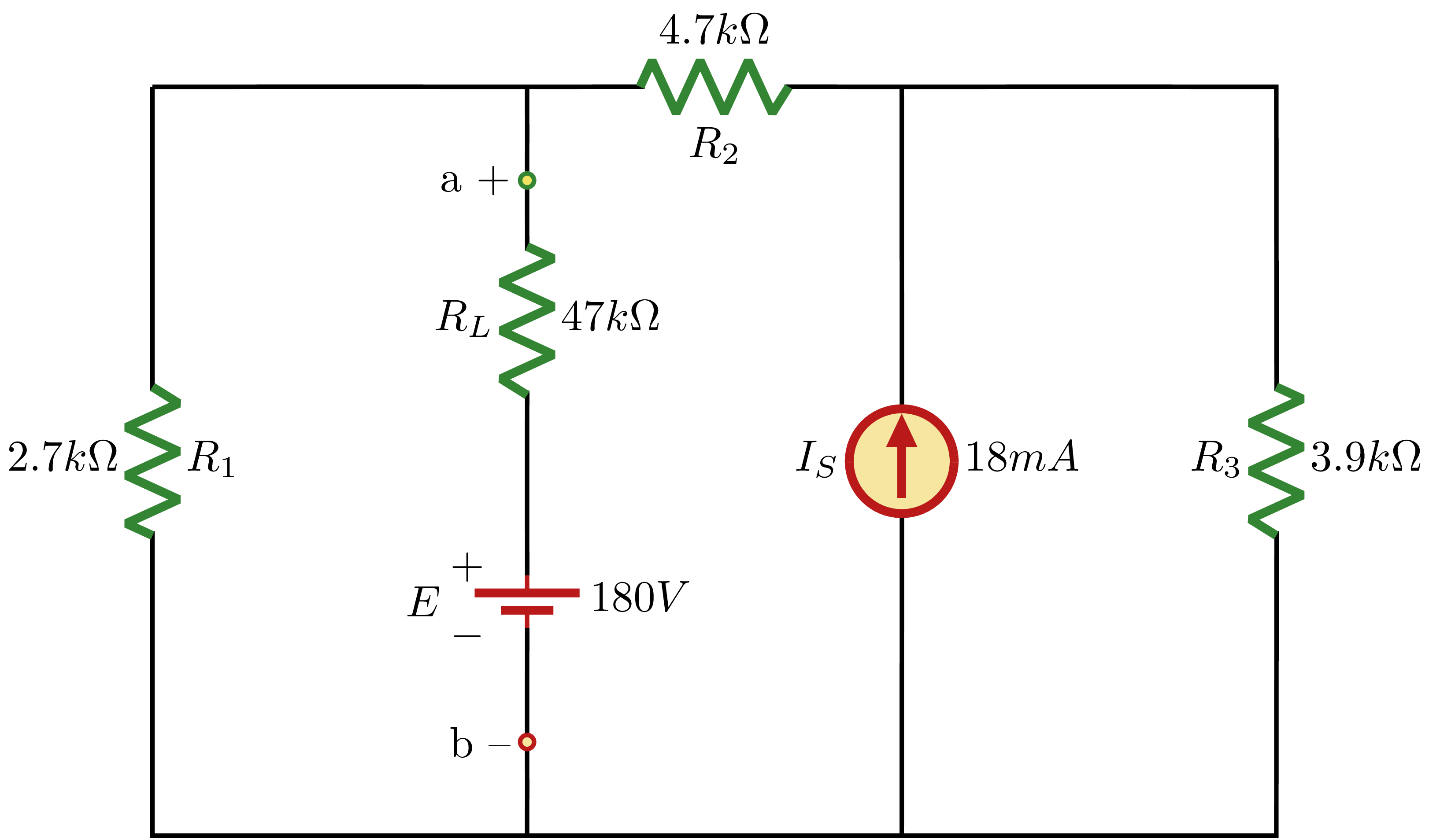
$$\begin{align}
R_{N} &= R_1 //(R_2 + R_3)\\
&= \frac{(2.7k\Omega) \cdot (4.7k\Omega+3.9k\Omega)}{(2.7k\Omega) + (4.7k\Omega + 3.9k\Omega)} \\
&= \frac{(2.7) \cdot (8.6)}{11.3}k\Omega \\
&=2.055k\Omega
\end{align}
$$

Solving for $I_N$

$$\begin{align}
\text{Using current divider rule:} \rightarrow I_{N} &= \frac{R_3}{R_2 + R_3}\cdot I_s\\
&= \frac{3.9k\Omega}{4.7k\Omega + 3.9k\Omega}\cdot 18mA\\
&= 0.4535\cdot 18mA\\
&=8.163mA
\end{align}
$$

Using Norton theorem, find the equivalent Norton circuit for the highlighted circuit aross terminals a-b.

Solving for mesh currents using calculator

Using Norton theorem, find the equivalent Norton circuit for the highlighted circuit aross terminals a-b.

Solving for mesh currents using calculator