Using superposition, find the current through $R_1$
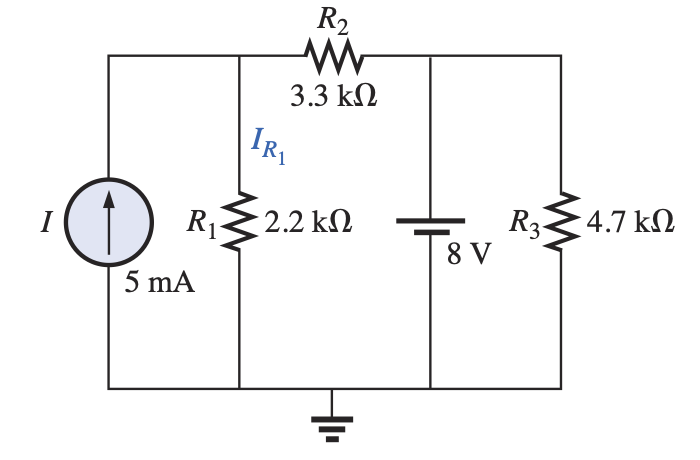
Simulation:
Using simulation as a guide, the circuit parameters will be as in the figue below.
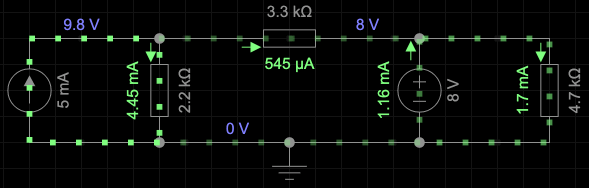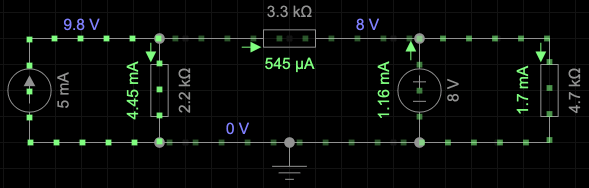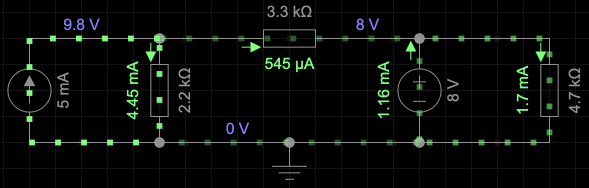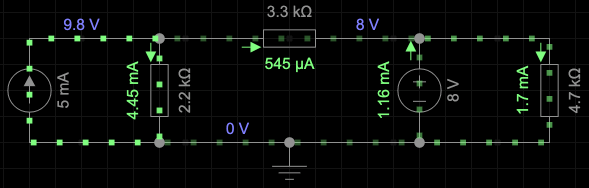
Solution:
The solution is in two parts. First we turn the battery off and solve for the current in $R_1$. The second part, we turn off the current source and solve for the curent through $R_1$ due to the battery.
Step 1: I (ON) E (OFF)
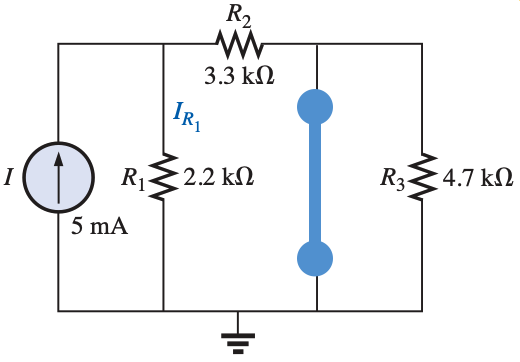
Note that $R_3$ is shorted, and to obtain the current through $R_1$ we will use the current divider rule:
$$\begin{align}\text{Current divider rule: }\rightarrow I'_{R_1} &= \frac{R_2}{(R_1+R_2)}\cdot I \\
&=\frac{3.3 k\Omega}{(2.2 k\Omega + 3.3k\Omega)}\cdot 5mA \\
&=\frac{3.3 k\Omega}{5.5 k\Omega }\cdot 5mA \\
&=0.6\cdot 5mA \\
&=3mA \end{align}$$
Step 2: I (OFF) E (ON)
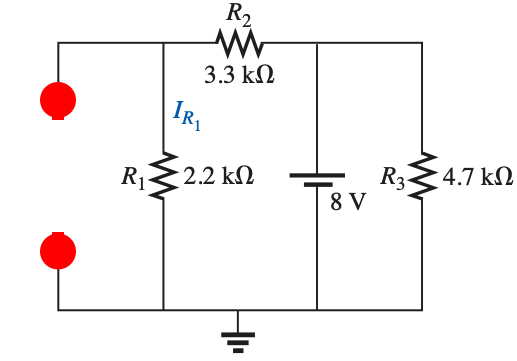
Since $R_3$ is in parallel with the battery, then the voltage across it is the battery voltage and it wont affect the current through $R_1$.
To solver for the current through $R_1$, we will only consider the resistances on the left side of the battery
$$\begin{align}\text{Ohm's Law: }\rightarrow I''_{R_1} &= \frac{E}{(R_1+R_2)}\\
&=\frac{8V}{(2.2 k\Omega + 3.3k\Omega)}\\
&=\frac{8V}{5.5 k\Omega }\\
&=1.455 mA \\
&=1.46 mA \end{align}$$
Step 3: Solving for $I_{R_1}$
$$\begin{align*}I_{R_1} &= I'_{R_1} + I''_{R_1} \\
&= 3 mA + 1.46 mA\\
&= 4.46 mA\end{align*}$$